IronIceandFire
Newbie
- Joined
- Dec 13, 2020
- Messages
- 10
Warning: it's about to get technical.
I've been looking around for a comprehensive and technical explanation of why discs fly the way they do and everything I've found has been either outright incorrect or not as technical as I wanted. Even if there is another good explanation out there, I want to make a good explanation easier to find on Google.
Therefore, I've compiled an explanation that to my knowledge shows technically how discs work. If any physicists out there catch any errors, please let me know, the last thing I want to do is look like a buffoon claiming that my wrong answer is right.
I should note that there is another post on this website about this topic, but 1) I want to use slightly more technical language and 2) I'm not confident that the effects it describes are entirely responsible for disc flight.
Part A: Rotational physics.
Here's a quick refresher on the physics of precession. Let's say you have a totally flat disc floating in space. When you spin the edge counter-clockwise, you are imparting a force F at a radius r. This creates a torque, T:
T = r x F
Using the right hand rule, point your four fingers along the radius of the disc and curl them towards the direction of force: your thumb points towards the torque vector. See Figure 1.
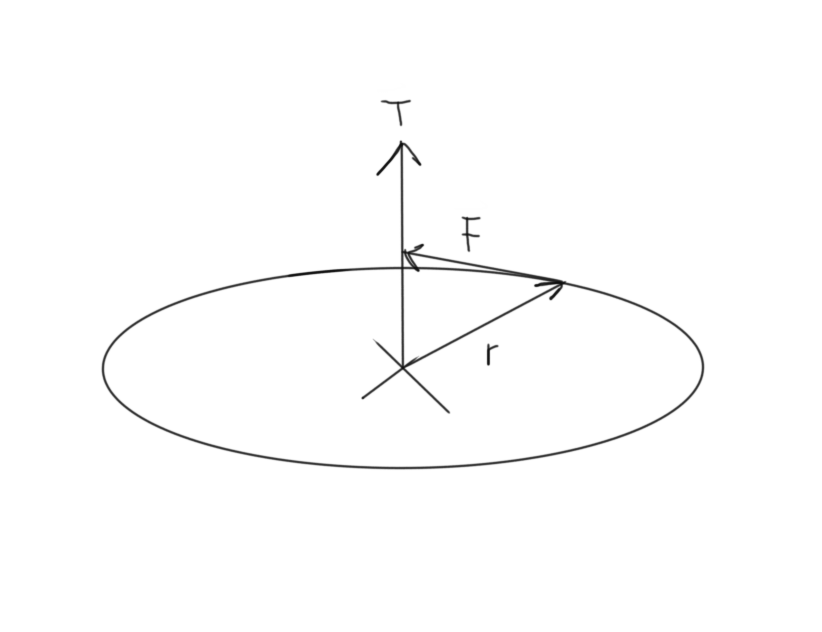
Figure 1.
Say the disc continues rotating counter-clockwise, and also has mass m. In this case, there is a velocity vector tangent to the disc at radius r. This creates an angular momentum, L:
L = m(r x v)
Similarly, point your four fingers on your right hand along the radius and curl towards the velocity: your thumb points towards the angular momentum vector. See Figure 2.
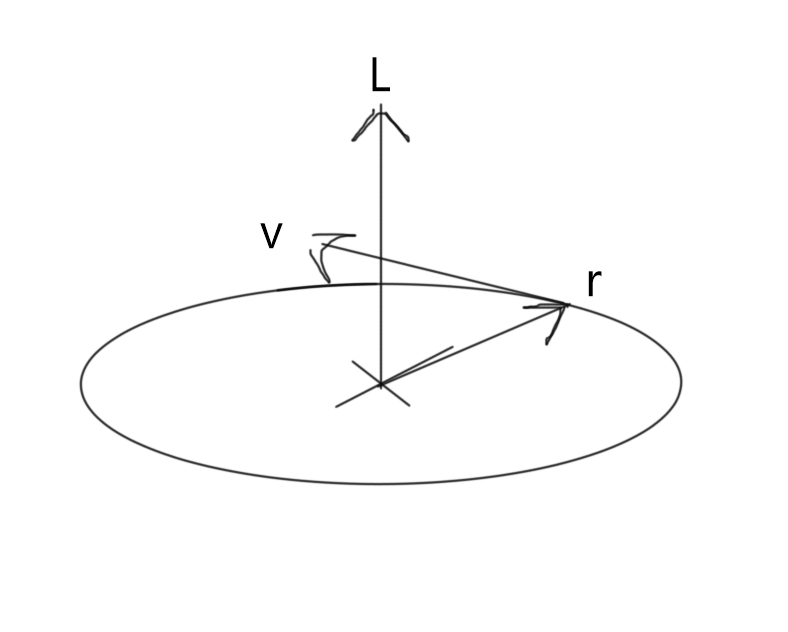
Figure 2.
Now, what happens if you put a force downward on the edge of the disc while it is spinning? First, we can establish that before you apply force, this disc has the same angular momentum of L. Then, our force at a radius creates a torque. This time, however, using the right hand rule we find that the torque, T, is along the radius of the disc. See Figure 3. In order to find the new angular momentum, we add the torque vector T and the previous angular momentum vector L (this is a simplification I think, but it works with the unit vectors and gives us the right idea). In Figure 3, this new angular momentum is Lnew.
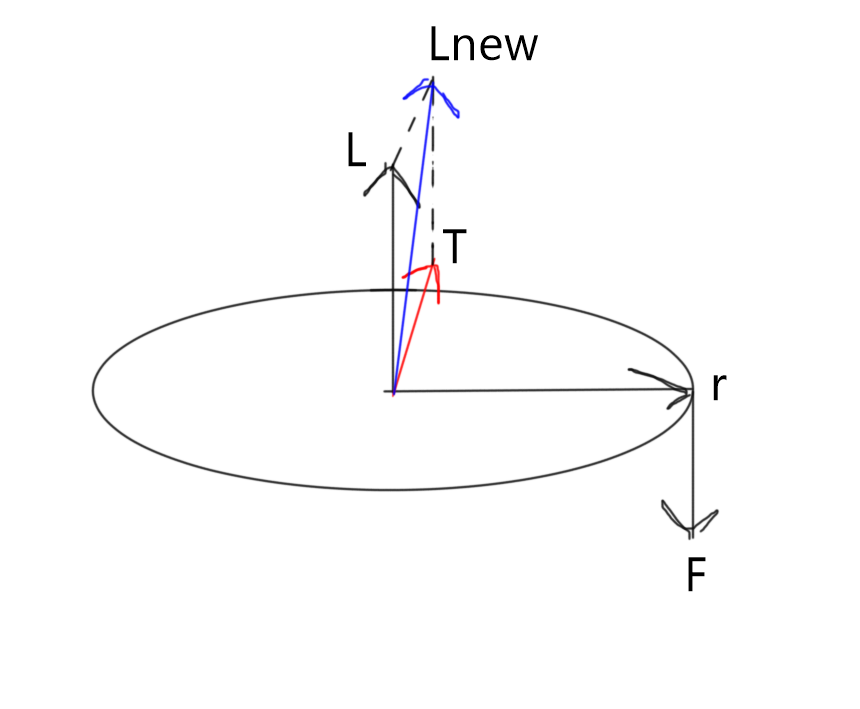
Figure 3.
This means that while force is being applied downwards on the right edge of a disc spinning counter-clockwise, it will pitch away from the viewer. If you don't believe me, try it! Spin a disc on your finger in that manner. If you tap the right edge of it while spinning, it will fall away from you.
Likewise, if that force is upwards, the disc will pitch towards the viewer.
Part B: Application to straight-flying discs.
In this section, assume that the disc is released with a velocity parallel to the ground and with its center axis orthogonal to the ground.
How does this affect disc flight? This is where parting line height (PLH) comes in. For our purposes, the parting line height will be the height at which the side of the disc begins to curve back towards the disc.
Figure 4 shows two extremes of PLH. Disc 1 has a PLH all the way at the top of the disc, and disc 2 has a PLH all the way at the bottom. Imagine both discs are released so that air is coming straight at them, as the figure shows.
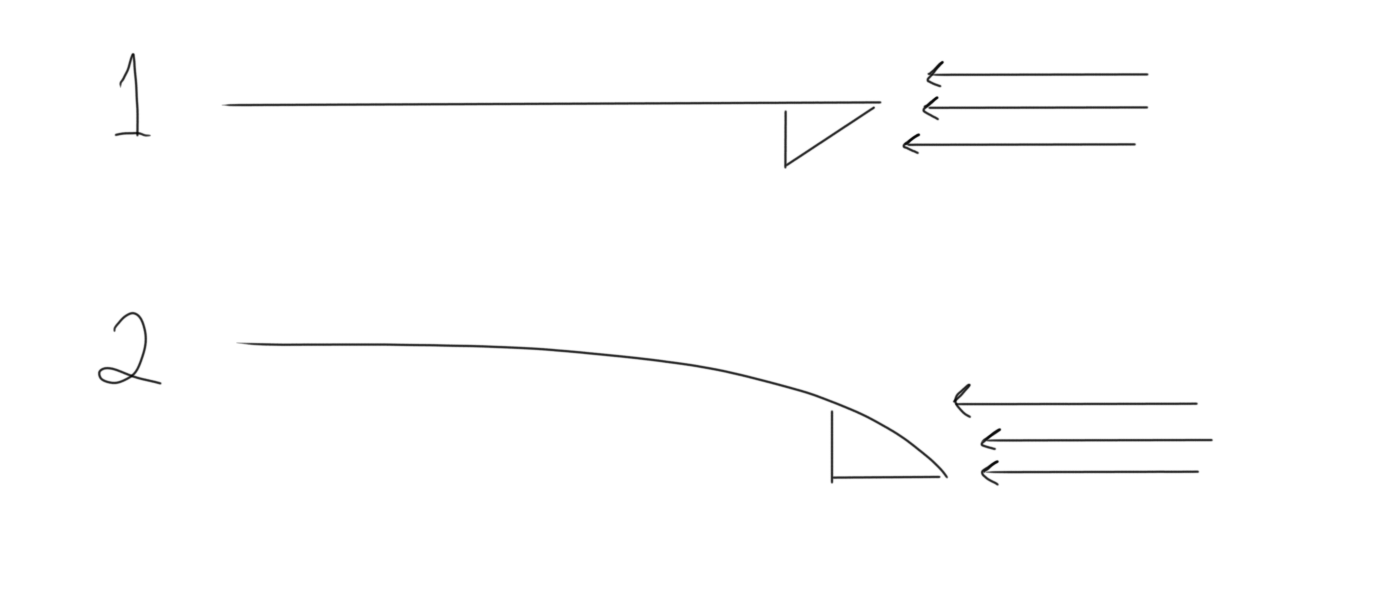
Figure 4.
Zooming in, imagine that air is made up of little individual frictionless balls, each of which behave about the same way (this is a valid assumption). Each ball has a velocity, Fair (mistakenly thought it was a force initially, bear with me). When it contacts the disc, it imparts a resultant force, Fr, which is perpendicular to the surface of the disc because there is no friction. See Figure 5.
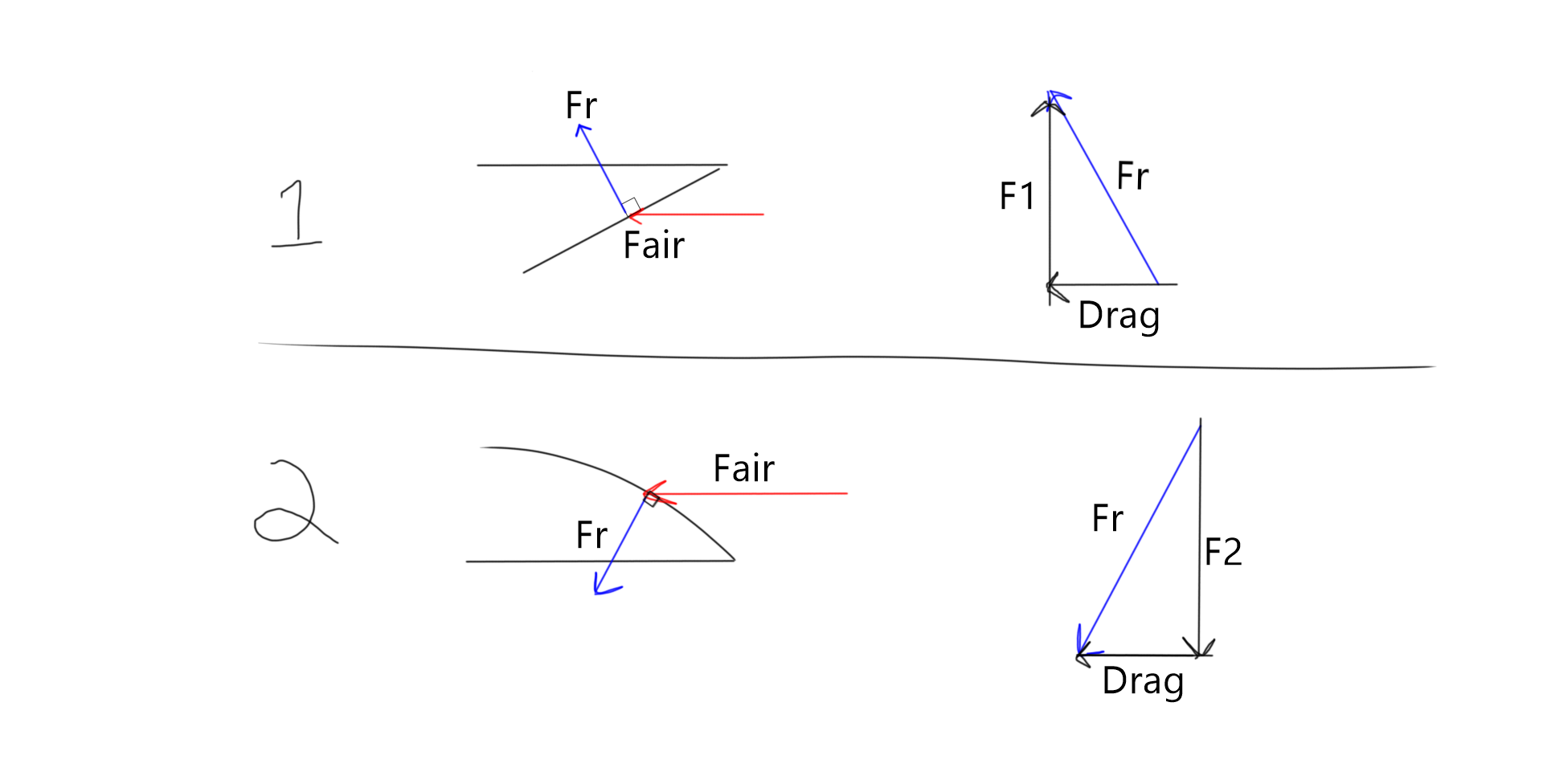
Figure 5.
Let's break down Fr for both disc shapes. For disc 1, there is a force upward, F1, and a force to the left, which is just drag. For disc 2, there is a force downward, F2, and drag. See Figure 5.
Remember what happens with a downward/upward force on the edge of a disc: it pitches forward or backward.
In this case, as a result of the forces applied to them from air, disc 1 will pitch towards from the viewer, and disc 2 will pitch away from the viewer. Disc 1 is OVERSTABLE, disc 2 is UNDERSTABLE.
This is why discs with a high PLH are overstable, and discs with a low PLH are understable.
Part C: Application to falling discs.
You may have seen a glaring omission in the previous section: if air causes (RHBH) understable discs to pitch right, how is it they can "recover" and fade left?
In this example, imagine that the disc is not traveling parallel to the ground, but rather is falling as it is traveling forwards, still orthogonal to the ground. In this case, air would not come straight at the side of the disc, but would come up at it. See Figure 6.
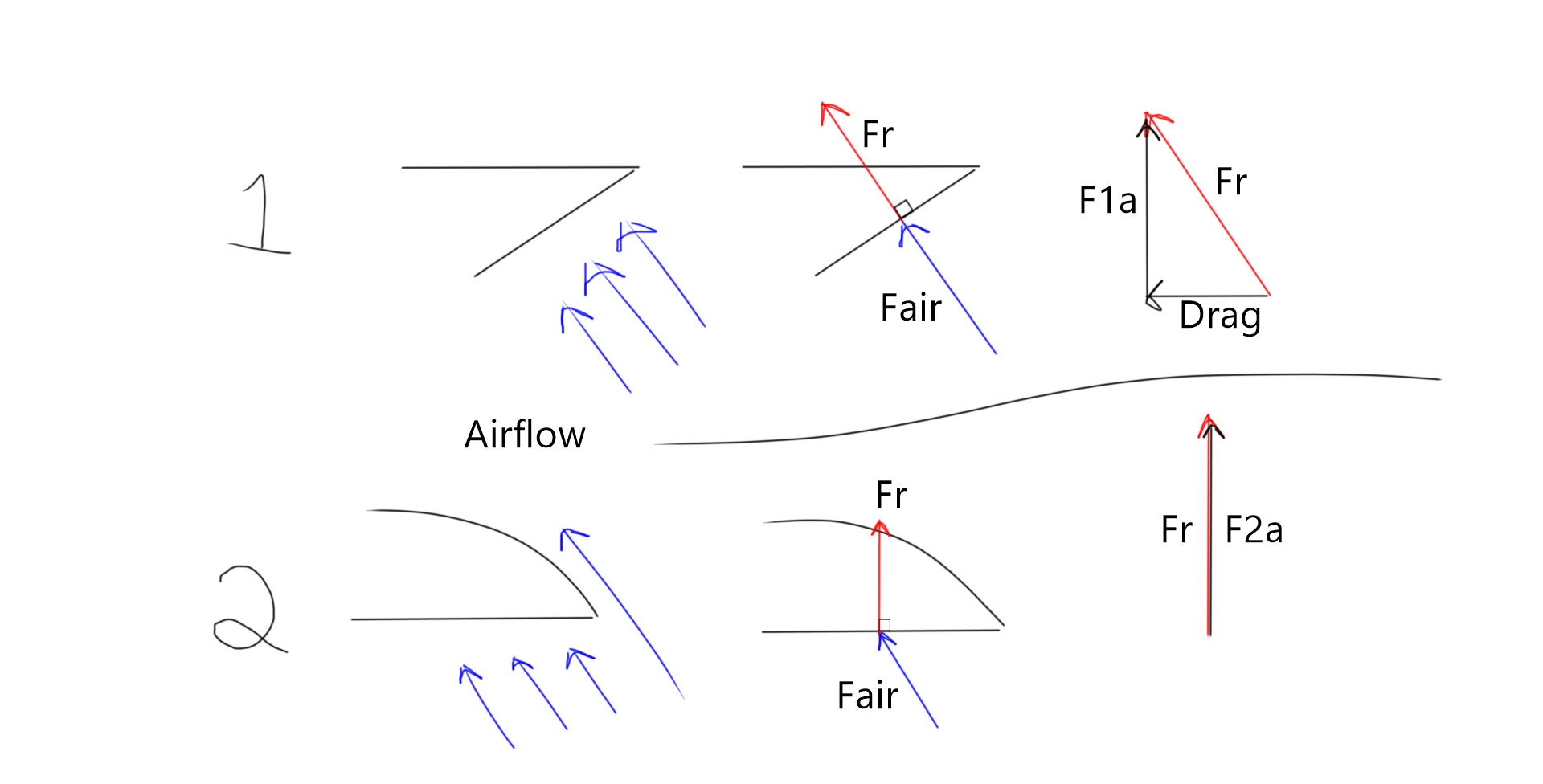
Figure 6.
The resultant force on disc 1 looks very similar to the previous example. However, the resultant force on disc 2 looks very different: again, the force on the disc is parallel to its surface because there is no friction. This time, however, that force is directly upwards because of the different angle of the disc's surface.
Let's break down Fr again. For disc 1, there is again a force upward, F1a, and drag. For disc 2, since the bottom of the disc was parallel to the ground, there is no drag, only an upward force. See Figure 6.
This time, both discs experience an upward force on their right edge while spinning counter-clockwise. This causes both discs to pitch towards the viewer.
This is why all discs act overstable at the end of their flight.
Part D: Application to rising discs.
How do discs glide any distance through the air? This is a result of Bernoulli's principle. This principle states that a high-velocity region of fluid will have a lower pressure than a low-velocity region of fluid.
When air flows over a disc, it has further to go when it passes under the disc than when it passes over a disc. As a result, the air is slowed down underneath the disc. Bernoulli's principle states that this slow air will have a higher pressure than the fast air over the disc. As a result, the disc will feel a net force directly upward along its axis of rotation. See Figure 7. While this force is stronger than gravity, the disc will experience an upwards acceleration. The faster a disc is moving, the more lift it will experience.
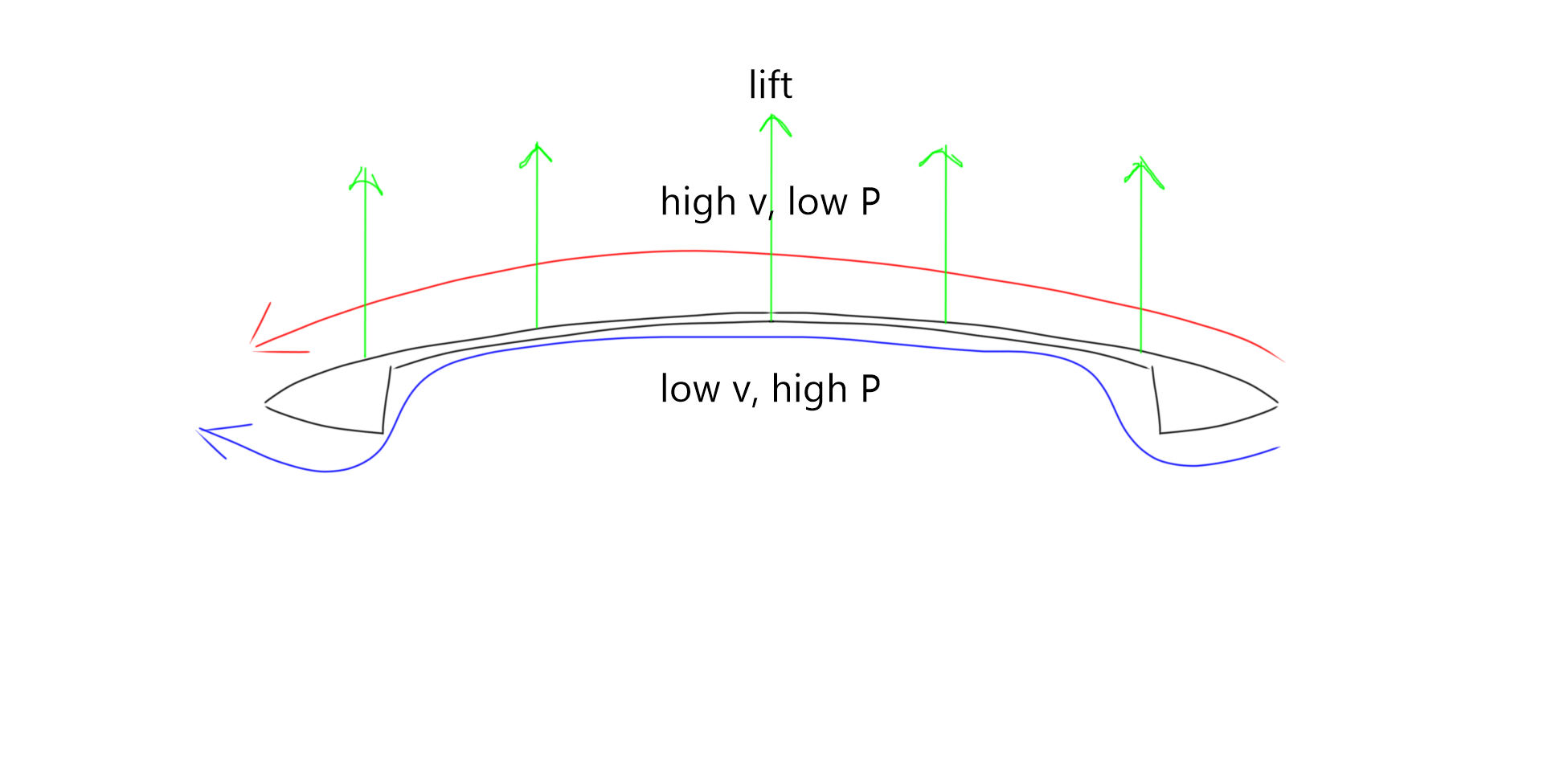
Figure 7.
Notably, this rising motion has the opposite effect of a falling motion, causing a disc to act more understable.
If discs never rose, they would immediately start falling, acting overstable. Because they experience lift, they not only can stay in the air longer, but also have time to act understable.
Discs act more understable when thrown faster because a) they experience more lift, making them act understable, and b) they don't fall as soon, giving them more time to act understable.
Discs act more understable when they are beaten in and when they are bent like a saddle because both phenomena force the PLH down, exposing more of the top of the disc.
Part E: What determines the fade of a disc.
So far, we have been talking about the shapes of different drivers, though the same principles can be applied to any disc shape (or any spinning object, for that matter). However, why are putters so different than drivers?
At the short ranges involved with putting, it is easiest to aim if the disc flies exactly the direction in which you threw it, and does not substantially fade to either side. What does this mean? It means that the same upward force on the edge of the disc has less effect on the angular momentum vector. In order to resist that force, the disc must have a higher moment of inertia. This is a measure of how hard an object is to spin. An ice skater with arms outstretched has a high moment of inertia, and because it is reduced when she brings her arms in, she is easier to spin, and spins faster.
How can a disc have "its arms outstretched"? This is the same question as "how can a disc have its weight further from its center axis"?
This is achieved by changing the shape of the edge of the disc. In Figure 8, assume the discs have the same weight, and assume that the weight of the edge in the red circle is the same for both. If we approximate the center of mass (com) of the weight in the red circle, we find that the com of the driver is closer to the center axis than the com of the putter. That is, rd is shorter than rp.
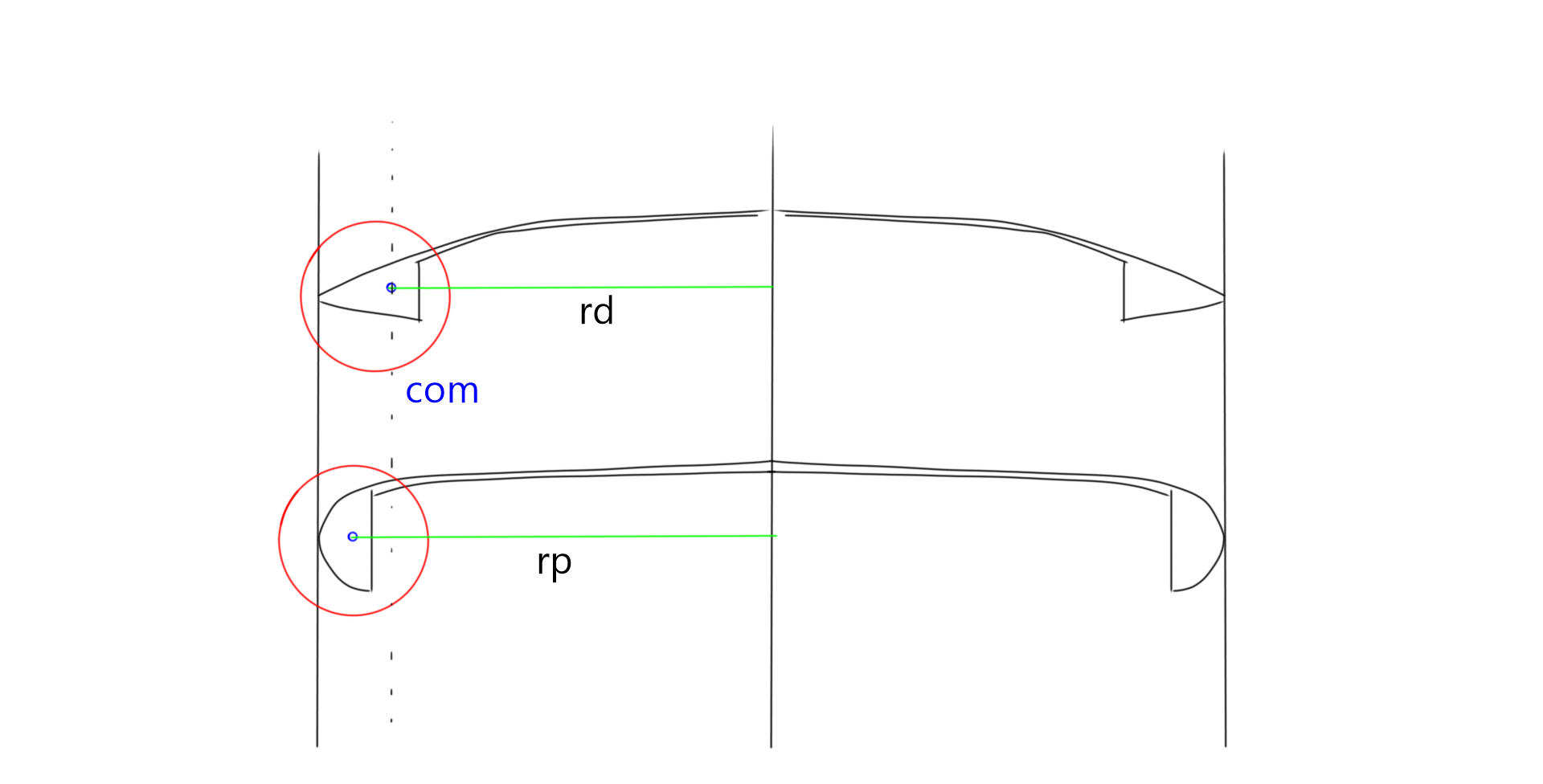
Figure 8.
As a result, the moment of inertia for a given driver is lower than that of a putter. Therefore, the putter will resist pitching from the forces of air more than the driver.
That is why putters fade less than drivers.
Conclusion
In case the photos don't show up in the post, here is a link to all of them: https://imgur.com/a/2CedRdV
There are a few things here I haven't mentioned. First, what determines the speed of a disc. I imagine this is simply a measure of its wind resistance, but I don't know.
Second, what determines the glide of a disc and why the bottom rim of some discs is curved. I imagine this is something to do with fluid dynamics, which I know very little about.
Third, the other post about physics on this website. Frankly, I didn't follow it very well because I couldn't see the figures. However, the parts I did understand were more or less based in good science, but would not create enough force to significantly affect the flight of a disc.
I've been looking around for a comprehensive and technical explanation of why discs fly the way they do and everything I've found has been either outright incorrect or not as technical as I wanted. Even if there is another good explanation out there, I want to make a good explanation easier to find on Google.
Therefore, I've compiled an explanation that to my knowledge shows technically how discs work. If any physicists out there catch any errors, please let me know, the last thing I want to do is look like a buffoon claiming that my wrong answer is right.
I should note that there is another post on this website about this topic, but 1) I want to use slightly more technical language and 2) I'm not confident that the effects it describes are entirely responsible for disc flight.
Part A: Rotational physics.
Here's a quick refresher on the physics of precession. Let's say you have a totally flat disc floating in space. When you spin the edge counter-clockwise, you are imparting a force F at a radius r. This creates a torque, T:
T = r x F
Using the right hand rule, point your four fingers along the radius of the disc and curl them towards the direction of force: your thumb points towards the torque vector. See Figure 1.

Figure 1.
Say the disc continues rotating counter-clockwise, and also has mass m. In this case, there is a velocity vector tangent to the disc at radius r. This creates an angular momentum, L:
L = m(r x v)
Similarly, point your four fingers on your right hand along the radius and curl towards the velocity: your thumb points towards the angular momentum vector. See Figure 2.

Figure 2.
Now, what happens if you put a force downward on the edge of the disc while it is spinning? First, we can establish that before you apply force, this disc has the same angular momentum of L. Then, our force at a radius creates a torque. This time, however, using the right hand rule we find that the torque, T, is along the radius of the disc. See Figure 3. In order to find the new angular momentum, we add the torque vector T and the previous angular momentum vector L (this is a simplification I think, but it works with the unit vectors and gives us the right idea). In Figure 3, this new angular momentum is Lnew.

Figure 3.
This means that while force is being applied downwards on the right edge of a disc spinning counter-clockwise, it will pitch away from the viewer. If you don't believe me, try it! Spin a disc on your finger in that manner. If you tap the right edge of it while spinning, it will fall away from you.
Likewise, if that force is upwards, the disc will pitch towards the viewer.
Part B: Application to straight-flying discs.
In this section, assume that the disc is released with a velocity parallel to the ground and with its center axis orthogonal to the ground.
How does this affect disc flight? This is where parting line height (PLH) comes in. For our purposes, the parting line height will be the height at which the side of the disc begins to curve back towards the disc.
Figure 4 shows two extremes of PLH. Disc 1 has a PLH all the way at the top of the disc, and disc 2 has a PLH all the way at the bottom. Imagine both discs are released so that air is coming straight at them, as the figure shows.

Figure 4.
Zooming in, imagine that air is made up of little individual frictionless balls, each of which behave about the same way (this is a valid assumption). Each ball has a velocity, Fair (mistakenly thought it was a force initially, bear with me). When it contacts the disc, it imparts a resultant force, Fr, which is perpendicular to the surface of the disc because there is no friction. See Figure 5.

Figure 5.
Let's break down Fr for both disc shapes. For disc 1, there is a force upward, F1, and a force to the left, which is just drag. For disc 2, there is a force downward, F2, and drag. See Figure 5.
Remember what happens with a downward/upward force on the edge of a disc: it pitches forward or backward.
In this case, as a result of the forces applied to them from air, disc 1 will pitch towards from the viewer, and disc 2 will pitch away from the viewer. Disc 1 is OVERSTABLE, disc 2 is UNDERSTABLE.
This is why discs with a high PLH are overstable, and discs with a low PLH are understable.
Part C: Application to falling discs.
You may have seen a glaring omission in the previous section: if air causes (RHBH) understable discs to pitch right, how is it they can "recover" and fade left?
In this example, imagine that the disc is not traveling parallel to the ground, but rather is falling as it is traveling forwards, still orthogonal to the ground. In this case, air would not come straight at the side of the disc, but would come up at it. See Figure 6.

Figure 6.
The resultant force on disc 1 looks very similar to the previous example. However, the resultant force on disc 2 looks very different: again, the force on the disc is parallel to its surface because there is no friction. This time, however, that force is directly upwards because of the different angle of the disc's surface.
Let's break down Fr again. For disc 1, there is again a force upward, F1a, and drag. For disc 2, since the bottom of the disc was parallel to the ground, there is no drag, only an upward force. See Figure 6.
This time, both discs experience an upward force on their right edge while spinning counter-clockwise. This causes both discs to pitch towards the viewer.
This is why all discs act overstable at the end of their flight.
Part D: Application to rising discs.
How do discs glide any distance through the air? This is a result of Bernoulli's principle. This principle states that a high-velocity region of fluid will have a lower pressure than a low-velocity region of fluid.
When air flows over a disc, it has further to go when it passes under the disc than when it passes over a disc. As a result, the air is slowed down underneath the disc. Bernoulli's principle states that this slow air will have a higher pressure than the fast air over the disc. As a result, the disc will feel a net force directly upward along its axis of rotation. See Figure 7. While this force is stronger than gravity, the disc will experience an upwards acceleration. The faster a disc is moving, the more lift it will experience.

Figure 7.
Notably, this rising motion has the opposite effect of a falling motion, causing a disc to act more understable.
If discs never rose, they would immediately start falling, acting overstable. Because they experience lift, they not only can stay in the air longer, but also have time to act understable.
Discs act more understable when thrown faster because a) they experience more lift, making them act understable, and b) they don't fall as soon, giving them more time to act understable.
Discs act more understable when they are beaten in and when they are bent like a saddle because both phenomena force the PLH down, exposing more of the top of the disc.
Part E: What determines the fade of a disc.
So far, we have been talking about the shapes of different drivers, though the same principles can be applied to any disc shape (or any spinning object, for that matter). However, why are putters so different than drivers?
At the short ranges involved with putting, it is easiest to aim if the disc flies exactly the direction in which you threw it, and does not substantially fade to either side. What does this mean? It means that the same upward force on the edge of the disc has less effect on the angular momentum vector. In order to resist that force, the disc must have a higher moment of inertia. This is a measure of how hard an object is to spin. An ice skater with arms outstretched has a high moment of inertia, and because it is reduced when she brings her arms in, she is easier to spin, and spins faster.
How can a disc have "its arms outstretched"? This is the same question as "how can a disc have its weight further from its center axis"?
This is achieved by changing the shape of the edge of the disc. In Figure 8, assume the discs have the same weight, and assume that the weight of the edge in the red circle is the same for both. If we approximate the center of mass (com) of the weight in the red circle, we find that the com of the driver is closer to the center axis than the com of the putter. That is, rd is shorter than rp.

Figure 8.
As a result, the moment of inertia for a given driver is lower than that of a putter. Therefore, the putter will resist pitching from the forces of air more than the driver.
That is why putters fade less than drivers.
Conclusion
In case the photos don't show up in the post, here is a link to all of them: https://imgur.com/a/2CedRdV
There are a few things here I haven't mentioned. First, what determines the speed of a disc. I imagine this is simply a measure of its wind resistance, but I don't know.
Second, what determines the glide of a disc and why the bottom rim of some discs is curved. I imagine this is something to do with fluid dynamics, which I know very little about.
Third, the other post about physics on this website. Frankly, I didn't follow it very well because I couldn't see the figures. However, the parts I did understand were more or less based in good science, but would not create enough force to significantly affect the flight of a disc.
